Questões Militares
Comentadas para ita
Foram encontradas 131 questões
Resolva questões gratuitamente!
Junte-se a mais de 4 milhões de concurseiros!
CONSTANTES

DEFINIÇÕES


No último livro que publicou em vida, Teia (1996), a escritora Orides Fontela escreveu o poema ao lado.

Podemos afirmar que:
I. nem a parte I nem a II indicam que o pássaro “joão-de-barro” pode ser visto como metáfora de um determinado tipo social.
II. apenas a parte III sugere que o trabalho feito pelo joão-de-barro aproxima-se daquele feito por um operário.
III. o poema, em seu todo, aproxima metaforicamente o “joão-de-barro” de um trabalhador brasileiro (um “João”, como o título indica).
IV. como no caso do pássaro, também para o operário vale a idéia de que o homem faz o trabalho e o trabalho faz o homem.
Estão corretas apenas as afirmações:
Na obra Quaderna (1960), João Cabral de Melo Neto incluiu um conjunto de textos, intitulado “Poemas da cabra”, cujo tema é o papel desse animal no universo social e cultural nordestino. Um desses poemas é reproduzido ao lado:
Um núcleo de cabra é visível
por debaixo de muitas coisas.
Com a natureza da cabra
Outras aprendem sua crosta.
Um núcleo de cabra é visível
em certos atributos roucos
que têm as coisas obrigadas
a fazer de seu corpo couro.
A fazer de seu couro sola.
a armar-se em couraças, escamas:
como se dá com certas coisas
e muitas condições humanas.
Os jumentos são animais
que muito aprenderam da cabra.
O nordestino, convivendo-a,
fez-se de sua mesma casta.
Acerca desse poema, NÃO se pode afirmar que:
Qual o dito popular que se aplica à situação mostrada na tira abaixo?

In August of 2000, a Japanese scientist named Toshiyuki Nakagaki announced that he had trained an amoebalike organism called slime mold to find the shortest route through a maze. Nakagaki had placed the mold in a small maze comprising four possible routes and planted pieces of food at two of the exits. Despite its being an incredibly primitive organism (a close relative of ordinary fungi) with no centralized brain whatsoever, the slime mold managed to plot the most efficient route to the food, stretching its body through the maze so that it connected directly to the two food sources. Without any apparent cognitive resources, the slime mold had “solved” the maze puzzle.
For such a simple organism, the slime mold has an impressive intellectual pedigree. Nakagaki’s announcement was only the latest in a long chain of investigations into the subtleties of slime mold behavior. For scientists trying to understand systems that use relatively simple components to build higher-level intelligence, the slime mold may someday be seen as the equivalent of the finches and tortoises that Darwin observed on the Galapagos Islands.
How did such a lowly organism come to play such an important scientific role? That story begins in the late sixties in New York City, with a scientist named Evelyn Fox Keller. A Harvard Ph.D. in physics, Keller had written her dissertation on molecular biology, and she had spent some time exploring the nascent field of “non-equilibrium thermodynamics”, which in later years would come to be associated with complexity theory. By 1968, she was working as an associate at Sloan-Kettering in Manhattan, thinking about the application of mathematics to biological problems. Mathematics had played such a tremendous role in expanding our understanding of physics, Keller thought – so perhaps it might also be useful for understanding living systems.
In the spring of 1968, Keller met a visiting scholar named Lee Segel, an applied mathematician who shared her interests. It was Segel who first introduced her to the bizarre conduct of the slime mold, and together they began a series of investigations that would help transform not just our understanding of biological development but also the disparate worlds of brain science, software design, and urban studies.
(…)
Johson, Steven. Emergence. Peguin Books Ltd. 2001, pp. 11-12.
In August of 2000, a Japanese scientist named Toshiyuki Nakagaki announced that he had trained an amoebalike organism called slime mold to find the shortest route through a maze. Nakagaki had placed the mold in a small maze comprising four possible routes and planted pieces of food at two of the exits. Despite its being an incredibly primitive organism (a close relative of ordinary fungi) with no centralized brain whatsoever, the slime mold managed to plot the most efficient route to the food, stretching its body through the maze so that it connected directly to the two food sources. Without any apparent cognitive resources, the slime mold had “solved” the maze puzzle.
For such a simple organism, the slime mold has an impressive intellectual pedigree. Nakagaki’s announcement was only the latest in a long chain of investigations into the subtleties of slime mold behavior. For scientists trying to understand systems that use relatively simple components to build higher-level intelligence, the slime mold may someday be seen as the equivalent of the finches and tortoises that Darwin observed on the Galapagos Islands.
How did such a lowly organism come to play such an important scientific role? That story begins in the late sixties in New York City, with a scientist named Evelyn Fox Keller. A Harvard Ph.D. in physics, Keller had written her dissertation on molecular biology, and she had spent some time exploring the nascent field of “non-equilibrium thermodynamics”, which in later years would come to be associated with complexity theory. By 1968, she was working as an associate at Sloan-Kettering in Manhattan, thinking about the application of mathematics to biological problems. Mathematics had played such a tremendous role in expanding our understanding of physics, Keller thought – so perhaps it might also be useful for understanding living systems.
In the spring of 1968, Keller met a visiting scholar named Lee Segel, an applied mathematician who shared her interests. It was Segel who first introduced her to the bizarre conduct of the slime mold, and together they began a series of investigations that would help transform not just our understanding of biological development but also the disparate worlds of brain science, software design, and urban studies.
(…)
Johson, Steven. Emergence. Peguin Books Ltd. 2001, pp. 11-12.
In August of 2000, a Japanese scientist named Toshiyuki Nakagaki announced that he had trained an amoebalike organism called slime mold to find the shortest route through a maze. Nakagaki had placed the mold in a small maze comprising four possible routes and planted pieces of food at two of the exits. Despite its being an incredibly primitive organism (a close relative of ordinary fungi) with no centralized brain whatsoever, the slime mold managed to plot the most efficient route to the food, stretching its body through the maze so that it connected directly to the two food sources. Without any apparent cognitive resources, the slime mold had “solved” the maze puzzle.
For such a simple organism, the slime mold has an impressive intellectual pedigree. Nakagaki’s announcement was only the latest in a long chain of investigations into the subtleties of slime mold behavior. For scientists trying to understand systems that use relatively simple components to build higher-level intelligence, the slime mold may someday be seen as the equivalent of the finches and tortoises that Darwin observed on the Galapagos Islands.
How did such a lowly organism come to play such an important scientific role? That story begins in the late sixties in New York City, with a scientist named Evelyn Fox Keller. A Harvard Ph.D. in physics, Keller had written her dissertation on molecular biology, and she had spent some time exploring the nascent field of “non-equilibrium thermodynamics”, which in later years would come to be associated with complexity theory. By 1968, she was working as an associate at Sloan-Kettering in Manhattan, thinking about the application of mathematics to biological problems. Mathematics had played such a tremendous role in expanding our understanding of physics, Keller thought – so perhaps it might also be useful for understanding living systems.
In the spring of 1968, Keller met a visiting scholar named Lee Segel, an applied mathematician who shared her interests. It was Segel who first introduced her to the bizarre conduct of the slime mold, and together they began a series of investigations that would help transform not just our understanding of biological development but also the disparate worlds of brain science, software design, and urban studies.
(…)
Johson, Steven. Emergence. Peguin Books Ltd. 2001, pp. 11-12.
De acordo com o texto, Evelyn Fox Keller
I. tornou-se PhD em Física pela Universidade de Harvard e foi a pioneira nos estudos sobre teoria de sistemas complexos.
II. acreditava na importância da Matemática não apenas para o estudo da Física, mas também da Biologia.
III. Influenciou as pesquisas do matemático Lee Segel, levando-o a se interessar pelo comportamento dos slime molds.
Está(ão) correta(s)
In August of 2000, a Japanese scientist named Toshiyuki Nakagaki announced that he had trained an amoebalike organism called slime mold to find the shortest route through a maze. Nakagaki had placed the mold in a small maze comprising four possible routes and planted pieces of food at two of the exits. Despite its being an incredibly primitive organism (a close relative of ordinary fungi) with no centralized brain whatsoever, the slime mold managed to plot the most efficient route to the food, stretching its body through the maze so that it connected directly to the two food sources. Without any apparent cognitive resources, the slime mold had “solved” the maze puzzle.
For such a simple organism, the slime mold has an impressive intellectual pedigree. Nakagaki’s announcement was only the latest in a long chain of investigations into the subtleties of slime mold behavior. For scientists trying to understand systems that use relatively simple components to build higher-level intelligence, the slime mold may someday be seen as the equivalent of the finches and tortoises that Darwin observed on the Galapagos Islands.
How did such a lowly organism come to play such an important scientific role? That story begins in the late sixties in New York City, with a scientist named Evelyn Fox Keller. A Harvard Ph.D. in physics, Keller had written her dissertation on molecular biology, and she had spent some time exploring the nascent field of “non-equilibrium thermodynamics”, which in later years would come to be associated with complexity theory. By 1968, she was working as an associate at Sloan-Kettering in Manhattan, thinking about the application of mathematics to biological problems. Mathematics had played such a tremendous role in expanding our understanding of physics, Keller thought – so perhaps it might also be useful for understanding living systems.
In the spring of 1968, Keller met a visiting scholar named Lee Segel, an applied mathematician who shared her interests. It was Segel who first introduced her to the bizarre conduct of the slime mold, and together they began a series of investigations that would help transform not just our understanding of biological development but also the disparate worlds of brain science, software design, and urban studies.
(…)
Johson, Steven. Emergence. Peguin Books Ltd. 2001, pp. 11-12.
Em sua pesquisa, Toshiyuki Nakagaki
I. colocou um slime mold num labirinto com quatro saídas.
II. treinou um slime mold a sair de um labirinto pelo caminho mais curto.
III. colocou alimentos em todas as saídas do labirinto para atrair o slime mold.
Está(ão) correta(s)
In August of 2000, a Japanese scientist named Toshiyuki Nakagaki announced that he had trained an amoebalike organism called slime mold to find the shortest route through a maze. Nakagaki had placed the mold in a small maze comprising four possible routes and planted pieces of food at two of the exits. Despite its being an incredibly primitive organism (a close relative of ordinary fungi) with no centralized brain whatsoever, the slime mold managed to plot the most efficient route to the food, stretching its body through the maze so that it connected directly to the two food sources. Without any apparent cognitive resources, the slime mold had “solved” the maze puzzle.
For such a simple organism, the slime mold has an impressive intellectual pedigree. Nakagaki’s announcement was only the latest in a long chain of investigations into the subtleties of slime mold behavior. For scientists trying to understand systems that use relatively simple components to build higher-level intelligence, the slime mold may someday be seen as the equivalent of the finches and tortoises that Darwin observed on the Galapagos Islands.
How did such a lowly organism come to play such an important scientific role? That story begins in the late sixties in New York City, with a scientist named Evelyn Fox Keller. A Harvard Ph.D. in physics, Keller had written her dissertation on molecular biology, and she had spent some time exploring the nascent field of “non-equilibrium thermodynamics”, which in later years would come to be associated with complexity theory. By 1968, she was working as an associate at Sloan-Kettering in Manhattan, thinking about the application of mathematics to biological problems. Mathematics had played such a tremendous role in expanding our understanding of physics, Keller thought – so perhaps it might also be useful for understanding living systems.
In the spring of 1968, Keller met a visiting scholar named Lee Segel, an applied mathematician who shared her interests. It was Segel who first introduced her to the bizarre conduct of the slime mold, and together they began a series of investigations that would help transform not just our understanding of biological development but also the disparate worlds of brain science, software design, and urban studies.
(…)
Johson, Steven. Emergence. Peguin Books Ltd. 2001, pp. 11-12.
O efeito de humor da tirinha abaixo se deve.

Quino

I. realçar ironicamente essas palavras.
II. retomar uma explicação dada anteriormente.
III. destacar que essas palavras não são peculiares ao estilo do autor.
Está(ão) correta(s) apenas:


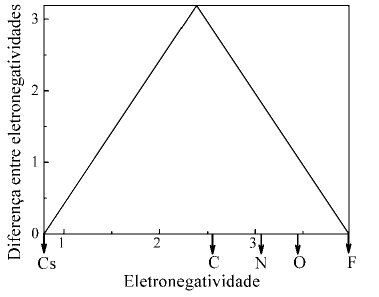
O par de pronomes que expressa a dicotomia dos conjuntos tribos/navegantes e tribos vizinhas/não navegantes é
 e
e  com origem no centro da Terra. É correto afirmar que
com origem no centro da Terra. É correto afirmar que
O módulo de Young de um material mede sua resistência a deformações causadas por esforços externos. Numa parede vertical, encontra-se engastado um sólido maciço de massa específica ρ e módulo de Young E, em formato de paralelepípedo reto, cujas dimensões são indicadas na figura. Com base nas correlações entre grandezas físicas, assinale a alternativa que melhor expressa a deflexão vertical sofrida pela extremidade livre do sólido pela ação do seu próprio peso.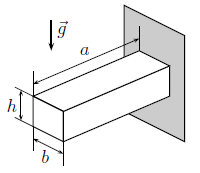

Acerca desse poema, é INCORRETO afirmar que
O poema abaixo, “Gioconda (Da Vinci)", de Carlos Drummond de Andrade, refere-se a uma célebre tela renascentista:

NÃO se pode afirmar que o poema
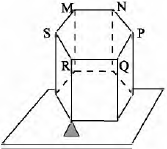
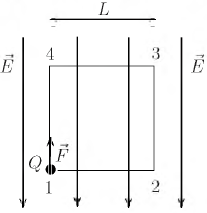
I. O trabalho da força F para deslocar a carga Q do ponto 1 para o ponto 2 é o mesmo dispendido no seu deslocamento ao longo do caminho fechado 1-2-3-4-1.
II. O trabalho da força F para deslocar a carga Q de 2 para 3 é maior que para deslocá-la da 1 para 2.
III. É nula a soma do trabalho da força F para deslocar a carga Q da 2 para 3 com seu trabalho para deslocá-la de 4 para 1.
Então, pode-se afirmar que