Questões Militares
Para vestibular
Foram encontradas 320 questões
Resolva questões gratuitamente!
Junte-se a mais de 4 milhões de concurseiros!
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos 
e 
, com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Considere as seguintes afirmações:
I. Se a medida do ângulo agudo entre uma reta r e um plano α é 45°, então existe uma reta s contida em α tal que a medida do ângulo agudo entre r e s é 30° .
II. Se uma reta r é perpendicular a duas retas distintas s e t contidas em um plano α, então r é perpendicular a α.
III. Sejam r, s e t as três retas distintas determinadas por três pontos não colineares. Então, existe um único ponto equidistante de r, s e t.
IV. Se P e Q são pontos à mesma distância de um plano α, então o ponto médio do segmento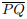 
pertence
a α.
É(são) VERDADEIRA(S):
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Seja ABCD um quadrilátero convexo com diagonais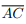 
e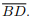 
Considere as afirmações:
I. Se as diagonais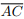 
e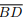 
têm mesmo comprimento e se intersectam ortogonalmente, então ABCD é
um losango.
II. Se as diagonais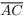 
e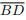 
dividem o quadrilátero ABCD em quatro triângulos de mesma área, então
ABCD é um paralelogramo.
III. Se o ponto de interseção das diagonais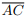 
e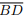 
é o centro do círculo que circunscreve o quadrilátero
ABCD, então ABCD é um retângulo.
É(são) VERDADEIRA(S):
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Seja A uma matriz real quadrada de ordem 2 tal que
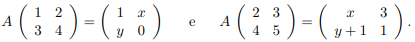
Então, o traço da matriz A é igual a:
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
A única solução real da equação
7x = 59x-1
pertence ao intervalo:
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
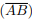= 14, cos 
=
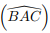3/5
e cos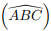 
=
5/13 .
Então, o raio da circunferência inscrita ao triângulo é igual a:
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
≤ 1. Podemos afirmar que Notações
ℕ = {1, 2, 3, . . . }: o conjunto dos números naturais.
ℝ : o conjunto dos números reais.
ℂ : o conjunto dos números complexos.
i : unidade imaginária, i2 = −1.
: segmento de reta de extremidades nos pontos A e B.
: ângulo formado pelos segmentos e , com vértice no ponto O.
m() : medida do segmento .
Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares.
I. (A + B)2 = A2 + 2AB + B2 . II. A comuta com qualquer matriz simétrica. III. B comuta com qualquer matriz antissimétrica. IV. det (A B) = 0.
É(são) VERDADEIRA(S):
A questão refere-se ao texto destacado a seguir.
When my family first moved to North Carolina, we lived in a rented house three blocks from the school where I would begin the third grade. My mother made friends with one of the neighbors, but one seemed enough for her. Within a year we would move again and, as she explained, there wasn’t much point in getting too close to people we would have to say good-bye to. Our next house was less than a mile away, and the short journey would hardly merit tears or even goodbyes, for that matter. It was more of a “see you later” situation, but still I adopted my mother’s attitude, as it allowed me to pretend that not making friends was a conscious choice. I could if I wanted to. It just wasn’t the right time.
Back in New York State, we had lived in the country, with no sidewalks or streetlights; you could leave the house and still be alone. But here, when you looked out the window, you saw other houses, and people inside those houses. I hoped that in walking around after dark I might witness a murder, but for the most part our neighbors just sat in their living rooms, watching TV. The only place that seemed truly different was owned by a man named Mr. Tomkey, who did not believe in television […].
To say that you did not believe in television was different from saying that you did not care for it. Belief implied that television had a master plan and that you were against it. It also suggested that you thought too much. When my mother reported that Mr. Tomkey did not believe in television, my father said, “Well, good for him. I don't know that I believe in it, either”.
“That's exactly how I feel,” my mother said, and then my parents watched the news, and whatever came on after the news.
SEDARIS, David. Dress Your Family in Corduroy and Denim. Recurso
eletrônico. Boston: Little, Brown and Company, 2004, p. 5.
A questão refere-se ao texto destacado a seguir.
When my family first moved to North Carolina, we lived in a rented house three blocks from the school where I would begin the third grade. My mother made friends with one of the neighbors, but one seemed enough for her. Within a year we would move again and, as she explained, there wasn’t much point in getting too close to people we would have to say good-bye to. Our next house was less than a mile away, and the short journey would hardly merit tears or even goodbyes, for that matter. It was more of a “see you later” situation, but still I adopted my mother’s attitude, as it allowed me to pretend that not making friends was a conscious choice. I could if I wanted to. It just wasn’t the right time.
Back in New York State, we had lived in the country, with no sidewalks or streetlights; you could leave the house and still be alone. But here, when you looked out the window, you saw other houses, and people inside those houses. I hoped that in walking around after dark I might witness a murder, but for the most part our neighbors just sat in their living rooms, watching TV. The only place that seemed truly different was owned by a man named Mr. Tomkey, who did not believe in television […].
To say that you did not believe in television was different from saying that you did not care for it. Belief implied that television had a master plan and that you were against it. It also suggested that you thought too much. When my mother reported that Mr. Tomkey did not believe in television, my father said, “Well, good for him. I don't know that I believe in it, either”.
“That's exactly how I feel,” my mother said, and then my parents watched the news, and whatever came on after the news.
SEDARIS, David. Dress Your Family in Corduroy and Denim. Recurso
eletrônico. Boston: Little, Brown and Company, 2004, p. 5.
A questão refere-se ao texto destacado a seguir.
When my family first moved to North Carolina, we lived in a rented house three blocks from the school where I would begin the third grade. My mother made friends with one of the neighbors, but one seemed enough for her. Within a year we would move again and, as she explained, there wasn’t much point in getting too close to people we would have to say good-bye to. Our next house was less than a mile away, and the short journey would hardly merit tears or even goodbyes, for that matter. It was more of a “see you later” situation, but still I adopted my mother’s attitude, as it allowed me to pretend that not making friends was a conscious choice. I could if I wanted to. It just wasn’t the right time.
Back in New York State, we had lived in the country, with no sidewalks or streetlights; you could leave the house and still be alone. But here, when you looked out the window, you saw other houses, and people inside those houses. I hoped that in walking around after dark I might witness a murder, but for the most part our neighbors just sat in their living rooms, watching TV. The only place that seemed truly different was owned by a man named Mr. Tomkey, who did not believe in television […].
To say that you did not believe in television was different from saying that you did not care for it. Belief implied that television had a master plan and that you were against it. It also suggested that you thought too much. When my mother reported that Mr. Tomkey did not believe in television, my father said, “Well, good for him. I don't know that I believe in it, either”.
“That's exactly how I feel,” my mother said, and then my parents watched the news, and whatever came on after the news.
SEDARIS, David. Dress Your Family in Corduroy and Denim. Recurso
eletrônico. Boston: Little, Brown and Company, 2004, p. 5.
A questão refere-se ao texto destacado a seguir.
When my family first moved to North Carolina, we lived in a rented house three blocks from the school where I would begin the third grade. My mother made friends with one of the neighbors, but one seemed enough for her. Within a year we would move again and, as she explained, there wasn’t much point in getting too close to people we would have to say good-bye to. Our next house was less than a mile away, and the short journey would hardly merit tears or even goodbyes, for that matter. It was more of a “see you later” situation, but still I adopted my mother’s attitude, as it allowed me to pretend that not making friends was a conscious choice. I could if I wanted to. It just wasn’t the right time.
Back in New York State, we had lived in the country, with no sidewalks or streetlights; you could leave the house and still be alone. But here, when you looked out the window, you saw other houses, and people inside those houses. I hoped that in walking around after dark I might witness a murder, but for the most part our neighbors just sat in their living rooms, watching TV. The only place that seemed truly different was owned by a man named Mr. Tomkey, who did not believe in television […].
To say that you did not believe in television was different from saying that you did not care for it. Belief implied that television had a master plan and that you were against it. It also suggested that you thought too much. When my mother reported that Mr. Tomkey did not believe in television, my father said, “Well, good for him. I don't know that I believe in it, either”.
“That's exactly how I feel,” my mother said, and then my parents watched the news, and whatever came on after the news.
SEDARIS, David. Dress Your Family in Corduroy and Denim. Recurso
eletrônico. Boston: Little, Brown and Company, 2004, p. 5.
A questão refere-se ao texto destacado a seguir.
It is the standing reproach of a democratic society that it is the purgatory of genius and the paradise of mediocrity. With ourselves it has become notorious that when a man is so unfortunate as to exhibit uncommon abilities, he usually renders himself ineligible for political honors or distinctions. It would seem that the community is possessed with that groveling quality of a sordid mind which hates superiority, and would ostracize genius, as the Athenians did Aristides. One might believe it would not be unpleasing to the popular taste if some enterprising person could invent a machine for stunting intellectual development, after the fashion of idiotic barbarians who flatten the heads of their children. The masses of the community certainly appear to believe that political equality implies not only social, but should also imply intellectual equality, under pain of being severely frowned down by an outraged public opinion.
The prevalent sentiment manifests itself in many different ways. It finds expression in public conveyances and resorts and is not altogether unknown even to the pulpit. It is found to perfection in the speeches of demagogues, who feel certain they are never so successful as when their audience is satisfied that the intellect of the speaker is of no higher an order than that of the lowest intelligence among them. Worse than all, it is demonstrated in the election of public officers of nearly all grades up to the highest: of which latter it has now become quite the custom to assume that it is impossible for a man of first-rate powers to be made President of the United States.
The causes which lend to so singular a state of affairs are of an intricate and complex character. At the outset, it is difficult to realize the possibility of a system, the logical deduction from which appears to be that, if a man would rise in life, he must assiduously belittle his understanding. Perhaps it would be fairer to modify the proposition so far as to concede that ability is as useful here as elsewhere, provided the owner has the tact not to affront the sensibilities of the people by showing too much of it. No doubt a vague apprehension exists in the popular mind that shining talents are dangerous when intrusted with executive power in a republic: yet, it were a poor commentary on our institutions to intimate that, under them, for a man to be clever he must also be vicious. Experience rather teaches the contrary. If the diffusion of education, having the general tendency to elevate the understanding, is to produce more bad men than good, we had better abandon than foster our Common School system. Manifestly, we must look further for the solution of our enigma[:] that minds of moderate calibre ordinarily condemn everything which is beyond their range.
THE NEW YORK TIMES. The worship of mediocrity. 17/08/1862.
Disponível em: https://www.nytimes.com/1862/08/17/archives/the-worship-of-mediocrity.html. Acesso 20/08/2020.
Conheça nossos planos